Lernauftrag 15: Berechnungen zum Kondensator durchführen
Hier findest du die Aufgaben ohne Lösungen.
Aufgabe 1
Der Kondensator hat eine Kapazität von \(C=47\ \mu F\) und soll an einer Wechselspannung \(U=110\ V, f=50\ Hz\) betrieben werden.
Berechne den Strom \(I\), der durch den Kondensator fließt.
geg: \(C=47\ \mu F, U=110\ V, f=50\ Hz\)
ges: \(I\)
Lös:
\(I=U\cdot 2\cdot\pi\cdot f\cdot C=110\ V\cdot 2\cdot \pi\cdot 50\ Hz\cdot 47\ \mu F\)
\(=110 \cancel{V}\cdot2\pi\cdot 50\frac{1}{\cancel{s}}\cdot47\cdot10^{-6}\frac{A\cancel{s}}{\cancel{V}}=1,624\ A\)
Aufgabe 2
Derselbe Kondensator wird mit einer Wechselspannung \(U=110\ V, f=60\ Hz\) betrieben.
Berechne erneut den Strom \(I\) durch den Kondensator.
Die Formel bleibt dieselbe, die Kürzungen ebenso und als Ergebnis kommt der Wert:
\(I=1,949\ A\)
Aufgabe 3
Erneut wird der Kondensator in anderer Umgebung eingesetzt. Er wird nun bei \(U=230\ V, f=50\ Hz\) betrieben.
Berechne auch hierfür den Strom \(I\) durch den Kondensator.
Die Formel bleibt dieselbe, die Kürzungen ebenso und als Ergebnis kommt der Wert:
\(I=3,396\ A\)
Aufgabe 4
Der Widerstand eines Kondensators beträgt \(67,7\ \Omega\), wenn er an Deutschlands Stromversorgung (\(230\ V, 50\ Hz\)) angeschlossen wird. Derselbe Kondensator soll danach in einem amerikanischen Netz (\(110\ V/60\ Hz\)) betrieben werden.
Vermute ausgehend von deinen vorherigen Berechnungen in Aufgabe 1 bis 3, ob der Widerstand des Kondensators steigt oder sinkt.
Hier gilt \(U_C=U\) da es nur den einen Kondensator gibt.
\(U=X_C\cdot I\Leftrightarrow X_C=\frac{U}{I}=\frac{U}{U\cdot 2\pi\cdot f\cdot C}=\frac{1}{2\pi\cdot f\cdot C}\Rightarrow X_C\sim\frac{1}{f}\)
Mit steigender Frequenz sinkt der Widerstand.
Aufgabe 5
Berechne den Widerstand des Kondensators, wenn er im amerikanischen Netz betrieben wird. Es kann hilfreich sein zuerst die Kapazität \(C\) des Kondensators auszurechnen.
\(I=U\cdot 2\cdot\pi\cdot f\cdot C\Leftrightarrow C=\frac{I}{U\cdot 2\pi\cdot f}\)
mit \(U=X_C\cdot I\Leftrightarrow \frac{I}{U}=\frac{1}{X_C}\) folgt
\(C=\frac{1}{X_C\cdot 2\pi\cdot f}=\frac{1}{67,7\ \Omega\cdot 2\pi\cdot 50\ Hz}=47\ \mu F\)
Umgestellt hatten wir früher schon
\(X_C=\frac{1}{2\pi\cdot f\cdot C}=\frac{1}{2\pi\cdot 60\ Hz\cdot 47\ \mu F}\)
\(=\frac{1}{2\pi\cdot 60\ Hz\cdot 47\cdot 10^{-6} F}=\frac{10^6}{2\pi\cdot 60\ Hz\cdot 47 F}\)
\(=56,44\ \Omega\)
Aufgabe 6
Ein \(100\ W\) Heizwiderstand \(R_{E1}\) am Wechselspannungsnetz \(230\ V/50\ Hz\) soll zur Energieeinsparung zeitweise nur mit halber Bemessungsleistung \(P\) betrieben werden. Anstelle eines ohmschen Vorwiderstandes soll dazu ein Kondensator \(\mathrm{C1}\) eingesetzt werden.
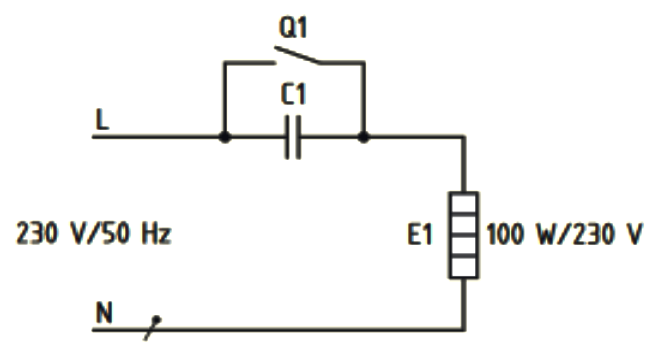
Berechne folgende Größen in dieser Reihenfolge
1) Bemessungswiderstand \(R_{E1}\)
2) Strom bei geöffnetem Schalter
3) Teilspannung \(U_R\) bei geöffnetem Schalter
4) kapazitiver Blindwiderstand
5) Kapazität von \(\mathrm{C1}\)
und zeichne anschließend das Zeigerbild der Spannungen.
Bemessungswiderstand \(R_{E1}\)
Mit \(U=R\cdot I \Leftrightarrow I=\frac{U}{R}\) eingesetzt in
\(P=U\cdot I=U\cdot\frac{U}{R}=\frac{U^2}{R}\Leftrightarrow R=\frac{U^2}{P}=\frac{(230\ V)^2}{100\ W}=529\ \Omega\)
Strom bei geöffnetem Schalter:
geg: \(P=50\ W, R=529\ \Omega\)
ges: \(I\)
Lös: \(P=U\cdot I=R\cdot I\cdot I\Leftrightarrow I=\sqrt{\frac{P}{R}}=\sqrt{\frac{50\ W}{529\ \Omega}}=307,44\ mA\)
Teilspannung \(U_R\) bei geöffnetem Schalter:
geg: \(I=307,44\ mA, R=529\ \Omega\)
ges: \(U_R\)
Lös: \(U_R=R\cdot I=529\ \Omega\cdot 307,44\ mA=162,64\ V\)
kapazitiver Blindwiderstand:
geg: \(U=230\ V, U_R=162,64\ V, I=307,44\ mA\)
\(X_C=\frac{U_C}{I}=\frac{\sqrt{U^2-U_R^2}}{I}=\frac{\sqrt{(230\ V)^2-(162,64\ V)^2}}{307,44\ mA}=528,98\ \Omega\)
Kapazität von \(\mathrm{C1}\):
\(C_1=\frac{1}{2\pi\cdot f\cdot X_C}=\frac{1}{2\pi\cdot 50\ Hz\cdot 528,98\ \Omega}=6,02\ \mu F\)
Zeigerbild:
\(U_C\) wurde bisher noch nicht explizit ausgerechnet, jedoch in der Berechnung von \(X_C\) bereits verwendet. Holen wir das ausrechnen nach:
\(U_C=\sqrt{U^2-U_R^2}=\sqrt{(230\ V)^2-(162,64\ V)^2}=162,63\ V\)
Da es sich um ein kapazitives Bauteil (Kondensator) handelt, eilt die Blindspannung \(U_C\) der Wirkspannung \(U_R\) nach.
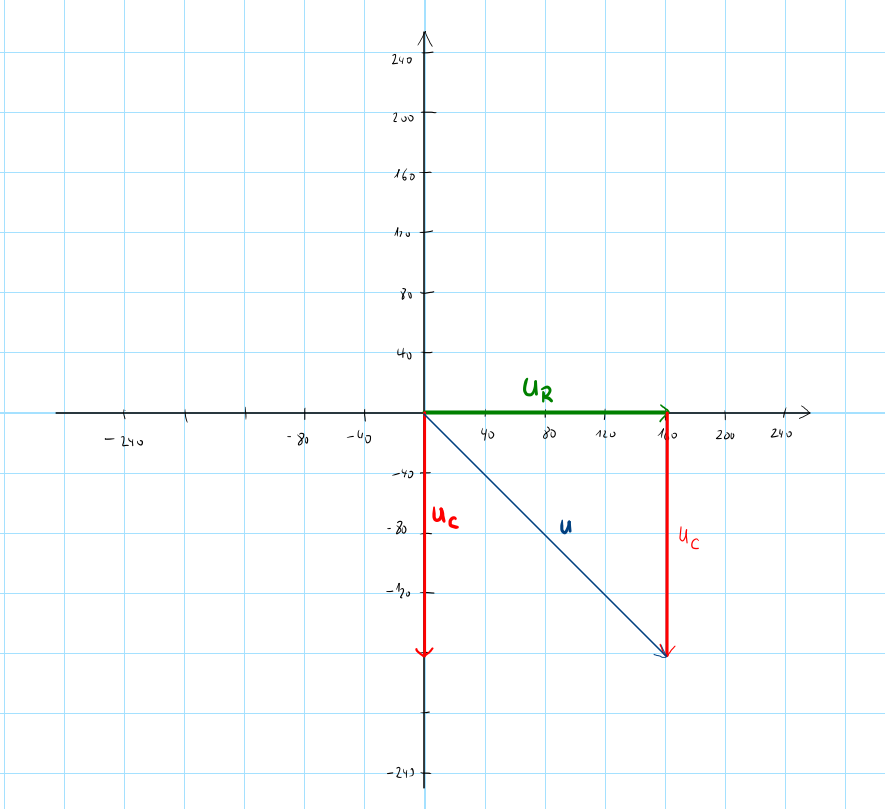
Alternativer Weg für die gesamte Aufgabe (für den Fall, daß es nur darum gegangen wäre die Kapazität des Bauteils zu bestimmen):
Die Wirkleistung des Heizwiderstandes soll sich von \(100\ W\) auf \(50\ W\) halbieren, also \(P=50\ W\). Somit muss die andere Hälfte der ursprünglichen \(100\ W\) Leistung in Blindleistung überführt werden und es gilt somit \(Q_L=50\ var\).
Für alle Dreiecke bedeutet dies sofort:
\(\varphi=45°\)
\(R_{E1}=X_C\)
\(U_R=U_C\)
\(P=Q_C\)
Wie in der obrigen Abfolge berechnen wir zuerst den Widerstand \(R_{E1}\) und wissen jedoch sofort, daß \(X_C\) diesselbe Größe hat. Mit \(Q_C\) können wir sofort die Kapazität des Kondensators berechnen, also:
Bemessungswiderstand \(R_{E1}\)
Mit \(U=R\cdot I \Leftrightarrow I=\frac{U}{R}\) eingesetzt in
\(P=U\cdot I=U\cdot\frac{U}{R}=\frac{U^2}{R}\Leftrightarrow R=\frac{U^2}{P}=\frac{(230\ V)^2}{100\ W}=529\ \Omega\)
\(\Rightarrow X_C=529\ \Omega\)
Kapazität von \(\mathrm{C1}\):
\(C_1=\frac{1}{2\pi\cdot f\cdot X_C}=\frac{1}{2\pi\cdot 50\ Hz\cdot 529\ \Omega}=6,02\ \mu F\)